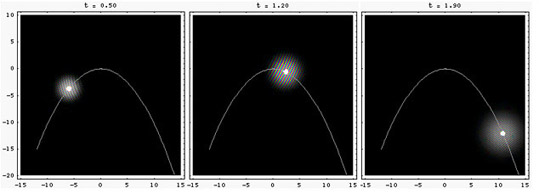
Dazu betrachten wir einen Vorgang, der uns allen im Alltag wohlbekannt ist:

Ein geworfener Tennisball

Ein in die Höhe geworfener Tennisball, der sich unter dem alleinigen Einfluß der Erdanziehung bewegt, fliegt auf einer sogenannten Wurfparabel. Vom Luftwiderstand wird abgesehen - bei der quantenmechanischen Bewegung einzelner Elektronen gibt es den auch gar nicht.

Die Bilder unten zeigen diese Wurfparabel als weiße Linie. Es handelt sich hier um Standbilder aus einem kurzen Film. Der weisse Punkt zeigt drei aufeinanderfolgende Positionen des Tennisballes. Am höchsten Punkt der Parabel ist die Bewegung am langsamsten. Wenn der Ball wieder zur Erde stürzt, gewinnt er kinetische Energie und wird schneller. Die horizontale Komponente der Geschwindigkeit (die Geschwindigkeit, die bei senkrechter Sonneneinstrahlung der Schatten am Boden haben würde) bleibt vom Anfang bis zum Ende gleich groß.

4

Ein geworfenes Elektron

Prinzipiell kann man auch ein einzelnes Elektron werfen. Da es so klein und leicht ist, ist die Handhabung und Beobachtung aber nicht ganz einfach. Es ist leichter, das Gravitationsfeld durch ein elektrisches Feld zu ersetzen. Elektronen sind elektrisch geladen und können in konstanten elektrischen Feldern leicht auf Parabelbahnen gezwungen werden. Die Bewegung ist gar nicht so verschieden von der gerade beschriebenen Wurfbewegung.

Die drei Bilder sind Standbilder eines Filmes, der eine Lösung der Schrödingergleichung für diese Situation zeigt. Die unscharfe Wolke, die sich um die klassisch-mechanische Position des Elektrons konzentriert, ist die quantenmechanische Wellenfunktion. Sie beschreibt die Aufenthaltswahrscheinlichkeit des quantenmechanischen Teilchens.