Ebene Wellen

Eine Welle ist ein zeitlich und räumlich periodischer Vorgang, der durch eine Wellenlänge und eine Frequenz charakterisiert wird. Eine solche Welle ist also per definitionem unendlich weit ausgedehnt. (Man bezeichnet so etwas als eine "ebene Welle"). Auch die Schrödingergleichung hat solche unendlich ausgedehnten Lösungen. Diese schauen dann etwa so aus:

-> Film (QuickTime, 690KB)

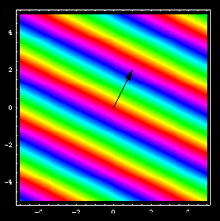
In diesem zweidimensionalen Abbild sehen wir eine Lösung der Schrödingergleichung. Sie hat überall die gleiche Intensität, ist also zeitlich und räumlich unendlich ausgedehnt. Die komplexe Phase der Welle (also die Farbe der Wellenfunktion) ist zeitlich und räumlich periodisch. Die deBroglie-Wellenlänge ist der Abstand zwischen zwei gleichfarbigen Streifen, also zum Beispiel zwischen zwei roten Streifen. Der Wellenvektor (schwarzer Pfeil) zeigt in Bewegungsrichtung der Welle. Diese ist immer senkrecht zu den Farblinien (im dreidimensionalen Raum wären das Farbflächen). An den Farben können wir die Bewegungsrichtung als Richtung von rot über gelb zu grün erkennen.

Nach deBroglie soll also ein solcher Wellenvorgang etwas mit der Bewegung eines Elektrons zu tun haben. Eine wirklich gewagte Hypothese! Von allem, was für die Bewegung eines Tennisballes charakteristisch ist, ist nur noch Bewegungsrichtung und Geschwindigkeit übriggeblieben. Der ganze Vorgang enthält gar nichts mehr vom Ort des Teilchens - die ebene Welle ist ja unendlich ausgedehnt. Wenn das schon die ganze Wahrheit wäre, könnten wir nicht verstehen, warum wir überhaupt jemals ein lokalisiertes Teilchen beobachten können.

Die Antwort auf diese Fragen steckt in der Schrödingergleichung. Und sie wird uns die Heisenbergsche Unschärferelation verständlich machen. Zunächst aber beschäftigen wir uns noch ein wenig mit den charakteristischen Merkmalen von quantenmechanischen Wellen.

10