09
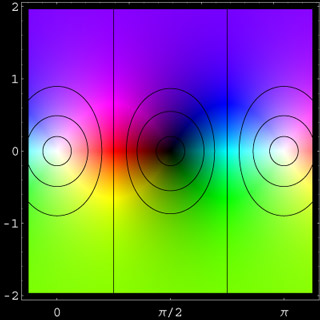
cot(z)
The complex cotangent function is defined (like in the real case) as cot(z) = 1/tan(z) = cos(z)/sin(z). Thus cot(z) has a zero wherever cos(z) has a zero and a pole wherever sin(z) has a zero. All zeros and poles are of first order and lie on the real axis. The image above shows contours at the absolute values 0.2, 0.5, 0.7, 1, 1.4, 2.2, and 5.
