23

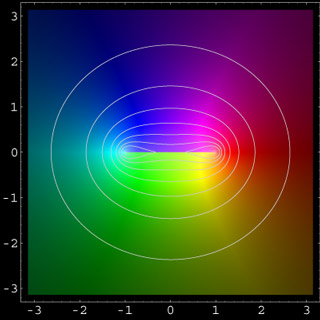
arccoth(z)

Inverse hyperbolic functions:

If z=coth(w) then w=arccoth(z) is called the inverse hyperbolic cotangent. It is a multivalued function. The image above shows the principal part, with a branch line between the points +1 and -1, where the function value approaches infinity. The relation with the logarithm is given by the formula

arccoth(z) = 1/2 ln( (z+1)/(z-1) )