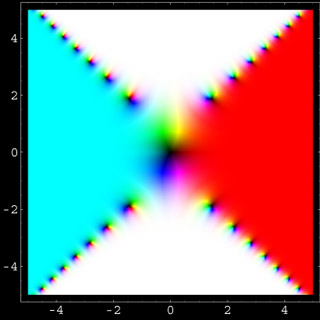
37
f(z) = erf(z)
The error function is the indefinite integral of the Gaussian function exp(-t2). It is used for many calculations in statistics. For real z, the error function is defined as
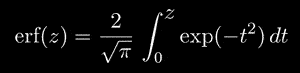
This function has an analytic continuation to the complex plane. The continuation can be defined via the power series representation
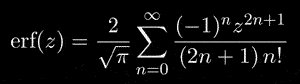
This is an entire analytic function without discontinuities or branch cuts. The error function has the symmetry properties erf(-z) = - erf(z) and erf(z*) = (erf(z))* (where the * denotes complex conjugation). Comprehensive information about the error function and related functions can be found in the Handbook of Mathematical Functions by Abramowitz and Stegun.
