Julian Grond and David Kammerlander:
Visualization of Bohmian Particles in One Dimension
Bohmian Mechanics is a deterministic interpretation of quantum mechanics, due to David Bohm, who searched for hidden variable theories. It is assumed that the position of a particle is a deterministic variable. The wavefunction evolves according to Schroedingers equation and in addition an equation of motion exists for the "Bohmian" particle
![]()
where j is the usual probability flux density of quantum mechanics and \rho the probability density.
For a detailed description visit http://bohm-c705.uibk.ac.at/.
For calculating the 1D-motion of a Bohmian particle for a given potential, we have to calculate the velocity field
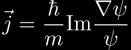
where \psi is the wave function of the particle. In Mathematica, we used the "Quantum Kernel" delivered by Prof. Thaller to compute the evolution of the wavefunction, which is Gaussian distributed initially and moves over a potential step or barrier. We discretize the wavefunction at each timestep and calculate the velocity field by numerical differentition. The motion of a particle initially located at a certain position is computed via Runge-Kutta of order 4 numerical integration.
In the movies we plot at once many particles, where the height at time zero suggests a Gaussian distribution of particles. The height loses its meaning later on, but the different height makes it easier to distinguish the particles. We see that a particle might either be reflected at the potential or transmitted, depending on the initial position.
- Scattering at a step (Mathematica notebook)
- QuickTime movies:
- Scattering at a smooth step (Mathematica notebook)
- QuickTime movies:
- Scattering at a rectangular barrier (Mathematica notebook)
- QuickTime movies:
