Komplexe Zahlen - ein mathematischer Ausflug
Die in den Visualisierungen sichtbaren Farben beschreiben komplexe Zahlen. Die Wellenfunktion ordnet jedem Punkt des Raumes und der Zeit eine komplexe Zahl zu. Was aber sind komplexe Zahlen?
Wir wollen die Details den Mathematikern überlassen. Für uns ist aber interessant, daß die komplexen Zahlen eigentlich zweidimensionale Objekte sind. Zum Unterschied von den gewöhnlichen, den reellen Zahlen, die sich auf einer Zahlengeraden anordnen lassen, benötigt die Menge der komplexen Zahlen die ganze zweidimensionale Ebene zur Visualisierung.
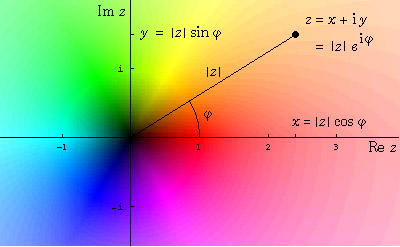
Jeder Punkt der Ebene steht für eine komplexe Zahl. Die gewöhnlichen reellen Zahlen kommen da auch vor, die horizontale Achse ist die gewohnte Zahlengerade. Zum Visualisieren geben wir jeder komplexen Zahl eine eindeutige Farbe.
Komplexe Zahlen haben einen Betrag (den Abstand von der komplexen Zahl Null, die die Farbe Schwarz bekommt). Der Betrag wird durch die Helligkeit der Farbe dargestellt. Die unendlich große komplexe Zahl bekommt dann die Farbe Weiß. Komplexe Zahlen werden auch noch durch ihre Phase beschrieben (im Bild oben ist das der Winkel der Betragsline mit der horizontalen Zahlengeraden). Die Phase wird durch den Farbton dargestellt. Leicht zu merken ist: Rot ist positiv reell. Die gelbgrünen und blauvioletten Farben entsprechen den sogenannten imaginären Zahlen (entlang der senkrechten Koordinatenachse der komplexen Zahlenebene).
Der mathematisch vorgebildete Leser hat jetzt vielleicht Freude an der Betrachtung einiger komplexwertiger (analytischer) Funktionen.
Quantenmechanische Wellenfunktionen haben an jedem Punkt des Raumes einen komplexen Zahlenwert. Würden wir das auf die sonst in der Mathematik üblichen Art mit Funktionsgraphen darstellen wollen, müßten wir im fünfdimensionalen Raum zeichnen können. Daher müssen wir die Farben zur Visualisierung verwenden. Mit einem einzigen Farbpunkt stellen wir also einen zweidimensionalen (komplexen) Datenwert dar.
|

