Interferenz
Die Überlagerung zweier Lösungen der Schrödingergleichung führt durch die Addition der komplexen Wellen zu ganz neuen Wellenformen. Bei dieser Superposition ist es entscheidend, daß die Wellenamplitude an jedem Raum- und Zeitpunkt einen komplexen Wert hat. Dadurch ist die Vielfalt der Ergebnisse viel größer, als es sonst möglich wäre. Die gegenseitige Beeinflussung der Wellenfunktionen bei der Überlagerung nennt man Interferenz.
Im folgenden Bild sieht man die Interferenz zweier ebener Wellen. Obwohl die einzelnen Wellenzüge überall die gleiche Intensität haben, hat der resultierende Wellenzug eine räumlich variierende Intensität.
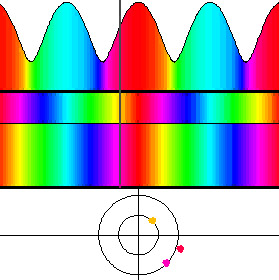
Die Überlagerung der ebenen Wellen geschieht durch vektorielle Addition der komplexen Zahlen. Wenn die beiden ebenen Wellen im selben Raumgebiet ähnliche Farben haben, addieren sich die Amplituden. Dort, wo sie komplementäre Farben haben, werden die Amplituden subtrahiert, löschen sich also gegenseitig aus.
Durch die Überlagerung vieler ebener Wellen können wir so ganz gut lokalisierte Wellenfunktionen herstellen:
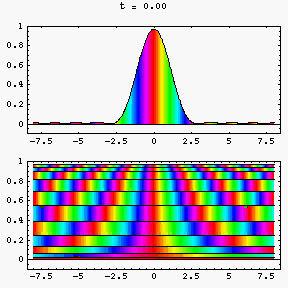
-> Film (QuickTime, 600KB)
Durch diesen Interferenzeffekt können wir Lösungen der Schrödingergleichung erzeugen, die in der Umgebung beliebig gewählter Orte lokalisiert sein können. Da ein Teilchen etwas ist, das wir uns als irgendwo lokalisiert vorstellen, können wir so den Schritt von den Wellen zur Beschreibung von Teilchen machen. Das lokalisierte Wellenpaket ist aber auf jeden Fall ein Zwitter aus Teilchen und Welle. Mit einem Teilchen hat es die mehr oder weniger gute Lokalisierung gemein, mit einer Welle die (komplexe) Phasenoszillation.
Der Preis für die Herstellung lokalisierter Wellenpakete ist der folgende: Wir können nicht mehr genau sagen, welche Wellenlänge das Ergebnis hat. Es sind ja ebene Wellen mit vielen verschiedenen Wellenlängen am Aufbau beteiligt. Physikalisch heißt das, wir können dem so entstehenden Wellenvorgang keine genaue Geschwindigkeit mehr zuordnen. Mit dem Gewinn an räumlicher Lokalisierung, ist uns die genau bestimmte Geschwindigkeit abhanden gekommen. Das ist die Essenz der Heisenbergschen Unschärferelation.
|

