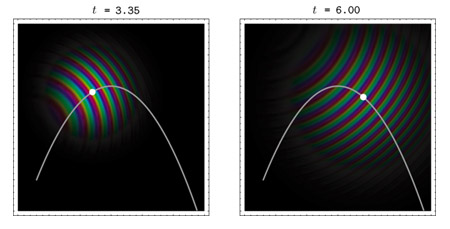
Die Unschärferelation

Wenn Sie bei den vorherigen Bildern genau hingesehen haben, ist Ihnen vielleicht aufgefallen, daß die Wellenfunktion im Laufe der Bewegung immer unschärfer wird: Der helle Fleck verbreitert sich im Laufe der Zeit. Das liegt daran, daß schon von allem Anfang an die Wellenfunktion eine nicht genau bekannte Geschwindigkeit hat. Genauso wie die möglichen Orte des Teilchens unscharf verteilt sind, so sind auch die Geschwindigkeiten nicht genau bestimmt - weder ist die Größe, noch die Richtung der Geschwindigkeit genau angebbar. Daher wird sich auch die anfängliche Ortsverteilung im Laufe der Zeit aufweiten.

Die Heisenberg'sche Unschärferelation (= Unbestimmtheitsrelation) besagt, daß das Produkt der Unschärfen von Ort und Geschwindigkeit für jede Wellenfunktion einen gewissen Mindestwert hat. Je genauer der Ort bestimmt ist, desto ungenauer ist die Geschwindigkeit gegeben - und umgekehrt! Wenn wir die Geschwindigkeit genau kennen, dann können wir nichts über den Ort vorhersagen.

-> siehe Film (QuickTime,1.9MB)

Hier sehen wir wieder die klassische und die quantenmechanische Wurfbewegung. Diesmal aber sehen wir ein Teilchen mit kleinerer Masse bzw. ein Teilchen in einem schwächeren Kraftfeld (die Bewegung findet also bei geringerer Energie statt). In dieser Situation unterscheidet sich die Quantenmechanik viel stärker von der klassischen Mechanik. Die Unschärferelation wird viel stärker spürbar und das Wellenpaket verteilt sich auf einen sehr viel größeren Bereich. Aber auch die Verbreiterung während der Bewegung ist stärker, da die Verteilungen der Geschwindigkeiten so unscharf ist.

Die Farben in den Bildern und im Film beschreiben die eigentliche Wellennatur des Teilchens. In der Quantenmechanik ist jedes Teilchen einerseits ein Massenpunkt (bei einer Ortsmessung findet man ein Teilchen an einem bestimmten Ort) und andererseits hat seine Bewegung den Charakter einer Wellenausbreitung. Diese Welle wird eben durch die Wellenfunktion beschrieben, die hier im Bild gezeigt wird.

Beachten Sie: Ein Teilchen ist viel kleiner als seine Wellenfunktion. Tatsächlich ist ein Elektron, nach allem was wir heute wissen, punktförmig. Die Helligkeit der Wellenfunktion im Bild beschreibt die Verteilung der Orte, an denen man das Teilchen finden kann. Wenn das Teilchen bei einer Ortsmessung gefunden wird, dann wird es als punktförmiges Teilchen gefunden. Die Wellenfunktion ist keine "Materiewelle", also keine räumliche Verteilung der Masse. Die Wellenfunktion beschreibt die räumliche Verteilung der Aufenthaltswahrscheinlichkeit.

Die Verteilung der Farben in der Wellenfunktion hat mit der Geschwindigkeit zu tun.

6