01
f(z) = z
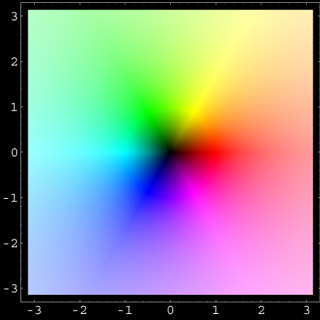
This is the complex plane where each point is colored according to the standard color map. We may interpret this image as a "colored density plot" of the identity f(z) = z.
In the colored density plot of a function f(z), each point z = x + iy of the complex plane receives a color that is determined by the complex number f(z).
The color defined by a complex number w is obtained as follows: The argument arg(w) of w determines the "hue", and the absolute value abs(w) determines the "lightness" of the color. The lightness ranges between zero (=black) at the origin (z=0) and one (=white) at the point "complex infinity". The standard Mathematica package Graphics`Colors` implements the color directive HLSColor which represents a color in the hue-lightness-saturation system. For the colormap of the complex plane we use only colors with maximal saturation (with respect to the HLS system). These colors correspond to the colors on the surface of the three-dimensional color manifold. Our color map of the complex plane is obtained by making a stereographic projection from the surface of the color manifold onto the complex plane. Notice that the surface of the three-dimensional compact color manifold is topologically homeomorphic to a sphere.
For the hues of complex numbers you should remember that red is positive real. Increasing hue-values (red, yellow, green, cyan, blue, magenta) correspond to increasing arguments. This defines the positive sense of rotation about the origin.
The additive primary colors red, green, blue correspond to the arguments 0, 2 Pi/3, and 4 Pi/3. The subtractive primary colors yellow, cyan (=blue+green), magenta (=blue+red), are at Pi/3, Pi, and 5 Pi/3. Hence the imaginary numbers with positive imaginary part correspond to colors between yellow and green. For all complex numbers w the negative number -w has the compementary color (red-cyan, yellow-blue, green-magenta etc).
All colors with a constant given lightness lie on a circle (with center at the origin) in the complex plane. As one can see above, yellow, cyan, and magenta appear much brighter than other colors with the same lightness. On a computer screen these colors are generated by adding two of the additive primary colors (red, green, blue) with maximal intensity.
The Mathematica software packages needed for colored density plots have been developed as a part of the project "Visual Quantum Mechanics".
