06
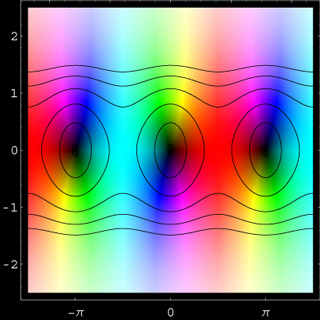
sin(z)
Show
3-d plot
The complex sine function has no singularity. It is analytic in the complex plane and is thus an entire analytic function. Its relation with the exponential function is given by sin(z) = [exp(iz)-exp(-iz)]/(2i). The only zeros of the complex sine function are on the real axis at 0, ±Pi, ±2Pi, .... (these are precisely the zeros of the ordinary sine function). The sine function is periodic in the x-direction, i.e., sin(z) depends periodically (with period 2Pi) on the real part of z. The contours are at the absolute values 0.1, 0.5, 0.9, 1.3, 1.7, and 2.1.
