07
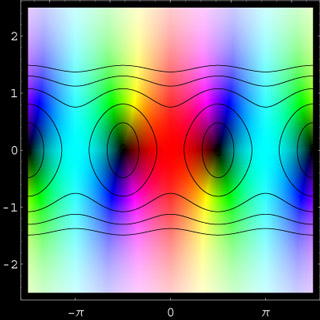
cos(z)
The complex cosine function differs from the sine function only by a translation in the x-direction. Its relation with the exponential function is given by sin(z) = [exp(iz)+exp(-iz)]/2. The complex cosine function has no singularities and all zeros are on the real axis where it coincides with the ordinary real cosine function. Like in the previous image, the contours visualize the absolute values 0.1, 0.5, 0.9, 1.3, 1.7, and 2.1.
