11

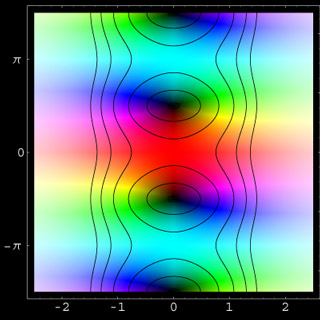
cosh(z)

Show
3-d plot

Hyperbolic functions:

The hyperbolic cosine is just given by cosh(z) = cos(iz). The "i" in the argument of cos causes a rotation of the image by 90 degrees. The definition in terms of the exponential function reads

cosh(z) = ( e^z + e^-z )/2 .