15
ln(z)
Show
3-d plot
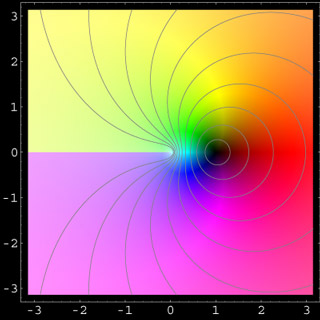
The complex natural logarithm is the inverse exponential function. If z = exp(w), then we write w = ln(z). In polar form, z=exp(ln r + i arg(z)), and hence the logarithm is given by
ln(z) = ln(r) + i arg(z)
Note that ln(z) is multiple valued, because the argument of a complex number z is not unique, unless restricted to an interval of length 2Pi. Here we show the principal part of the logarithm, which is defined by restricting the argument arg(z) to the interval [-Pi, Pi]. This choice corresponds to a branch-cut discontinuity along the negative real axis.
The complex logarithm has a singularity at z=0 (here the function value is infinite) and a zero at z=1. On the positive real axis, the complex logarithm coincides with the real logarithm.
