16

arcsin(z)

Show
3-d plot

Inverse trigonometric functions:

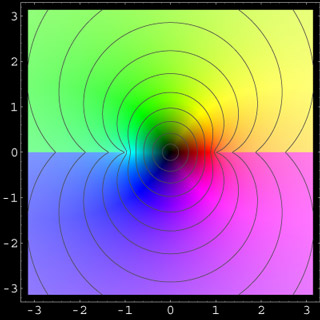
The image above shows the inverse of the sine function. If z=sin(w), then the inverse sine is given by w=arcsin(z). Like all inverse trigonometric functions, arcsin is multivalued. Here we show only the principal part, which is characterized by the property arcsin(0)=0. There are two branch lines extending along the real axis from ±1 to infinity. Since the sine function maps the real axis onto the interval [-1,1], the inverse function arcsin is well-defined and real-valued only on that interval of the real axis. Apart from z=0, arcsin has no zero in the complex plane. There are no points (except infinity) where the function value becomes infinity.