Größenvergleich der Wellenfunktionen, Grundzustand

---

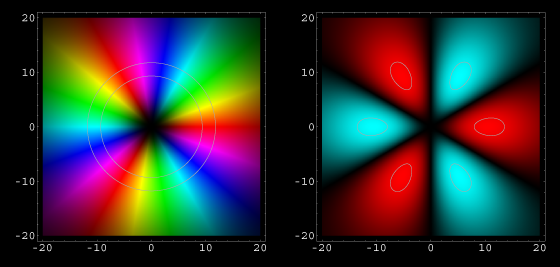
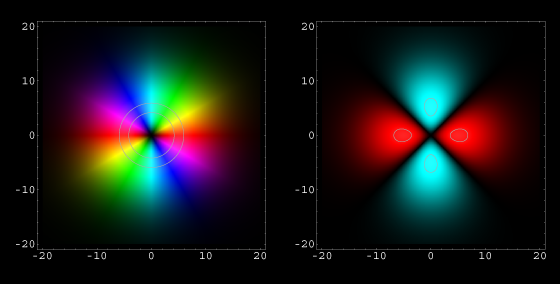
Diese Bilder zeigen wieder, von oben betrachtet, Wellenfunktionen, die sich mit einer bestimmten Anzahl von Wellenlängen bzw. Schwingungsknoten, um den (hier unsichtbaren) Atomkern herum gelegt haben. Alle Bilder haben den selben Abbildungsmaßstab, damit ein Größenvergleich möglich ist. Alle gezeigten Wellenfunktionen beschreiben stationäre Zustände: Die Aufenthaltswahrscheinlichkeit bleibt zeitlich konstant.

Abb. 1: Momentaufnahmen von Wellenfunktionen. Links: Ringförmige Wellenfunktionen. Rechts: Stationäre Schwingung, die durch Überlagerung der ringförmigen Wellenfunktion links und einer mit gegenläufiger Phase gebildet wird. Die eingezeichneten Contourlinien markieren die Bereiche mit der größten Aufenthaltswahrscheinlichkeit.

Wir sehen: Je weniger Wellenlängen (oder Schwingungsbäuche) um den Atomkern herum arrangiert sind, desto geringer ist der durchschnittliche Abstand des Elektrons vom Atomkern.

Die unterste Bildzeile in Abb.1 zeigt eine Wellenfunktion, bei der nur mehr eine einzige Wellenlänge vorhanden ist. Ist das der Zustand, bei dem das Elektron dem Atomkern am nächsten ist?

Nein!

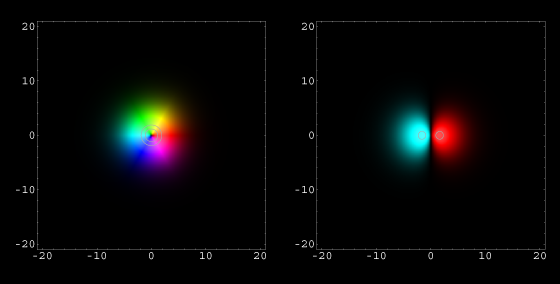
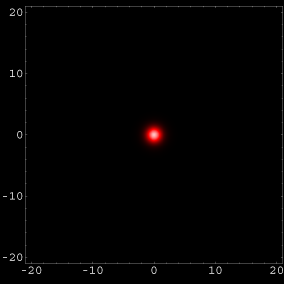
Tatsächlich gibt es einen Zustand ganz in der Nähe des Kernes. Er hat gar keine Schwingungsknoten und ist völlig kugelsymmetrisch. Hier sind Bilder davon:

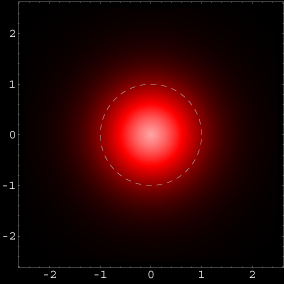
Abb .2: Zustand ohne Schwingungsknoten: Der Grundzustand. Links: Abbildung im Maßstab der Bilder oben. Rechts: Vergrößerte Abbildung. Die strichlierte Linie zeigt den sog. Bohr'schen Radius.

Die Wellenfunktion des Grundzustands kommt nicht durch eine Überlagerung von entgegengesetzt umlaufenden Wellen zustande. Ein Elektron, das durch diese Wellenfunktion beschrieben wird, vollführt keinerlei Kreisbewegung. Der Drehimpuls dieser Wellenfunktion ist Null.

Im Grundzustand ist der mittlere Abstand des Elektrons vom Atomkern der sogenannte Bohr'sche Radius. Er ist in Abb.2 links als strichlierte Kreislinie markiert. Die Länge des Bohr'schen Radius wird in der Atomphysik oft als Längeneinheit verwendet

Links: