Teilchendichte

Abbildung: Momentaufnahme einer Teilchenwolke mit inhomogener Teilchendichte. Links: Der Ort eines jeden Teilchens wird durch einen weißen Punkt markiert. Rechts: Die Ortsverteilung der Teilchen wird durch eine kontinuierliche Funktion, die Teilchendichte, beschrieben. Der Funktionswert wird durch einen Grauton visualisiert. Dunkel sind die Regionen mit geringer Teilchendichte, hell sind die Regionen, wo sich viele Teilchen aufhalten.

Wenn sehr viele Teilchen (typischerweise Milliarden) in einem Raumgebiet vorhanden sind, ist es sinnlos, den genauen Ort und die Bewegung eines jeden Teilchens beschreiben zu wollen. Man verwendet dann eine kontinuierliche Größe, die sogenannte Teilchendichte, um die örtliche Verteilung der Teilchen zu beschreiben.

Homogene Verteilung: Wir betrachten zunächst den Fall, dass die Teilchen im betrachteten Raumgebiet gleichmäßig verteilt sind. Das heißt: Unterteilen wir das Raumgebiet in lauter gleich große Teilstücke der Größe ∆V (wobei jedes Teilstück noch sehr viele Teilchen enthalten möge), so befinden sich in jedem Teilstück (im Rahmen der Zählgenauigkeit) die gleiche Zahl ∆N von Teilchen. Dann definiert man die Teilchendichte als den Quotienten

η = ∆N / ∆V.

Inhomogene Verteilung: Wenn die Teilchen nicht gleichmäßig verteilt sind, dann ndert sich die Teilchendichte von Ort zu Ort. Man beschreibt das durch eine ortsabhängige Funktion η(x) die an jedem Punkt x die dort vorherrschende Teilchendichte angibt. Mit Hilfe von η(x) kann also man die ungefähre Zahl der Teilchen berechnen, die sich in einem kleinen Volumen ∆V um den Punkt x befinden. Diese Anzahl ist ungefähr

∆N = η(x) ∆V

Die Beschreibung der Verteilung von punktförmigen Teilchen durch eine kontinuierliche Funktion η ist eine mathematische Idealisierung. Die obige Gleichung ist nur dann einigermaßen genau, wenn das Volumen ∆V einerseits so klein ist, dass die Funktion η an allen Punkten von ∆V ungefähr denselben Wert hat, wie an der Stelle x (also den Wert η(x)). Andererseits muss ∆V aber so groß sein, dass noch immer sehr viele Teilchen in diesem Volumenstück enthalten sind. Wenn η(x) ∆V zu klein ist, würde aufgrund der zufälligen Platzierung der Teilchen auch die Teilchenzahl ∆N starke zufällige Schwankungen aufweisen.

In einer Dimension kann die Teilchendichte durch einen Funktionsgraphen dargestellt werden. In der Ebene stellen wir die Teilchendichte durch eine Dichtegrafik dar.

Aufgabe:

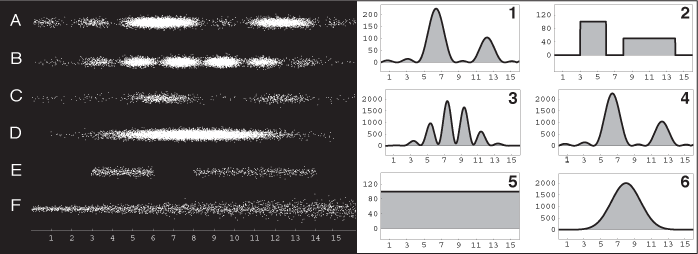
Teilchendichte in einer Dimension: Diese Abbildung zeigt links einige Beispiele von Teilchenstrahlen (Momentaufnahmen), bei denen die Teilchendichte variabel ist. Wir wollen die Teilchendichte längs des Teilchenstrahls durch eine Funktion beschreiben, die nur von der Koordinate entlang der Strahlrichtung abhängt. Die Dichteverteilung quer zur Strahlrichtung soll nicht beschrieben werden. Die Funktion soll nur angeben, wieviele Teilchen pro Längeneinheit sich am jeweiligen Ort im Strahl befinden. Rechts in der Abbildung befinden sich einige Beispiele von solchen Dichteverteilungen entlang von Teilchenstrahlen. Es ist die Aufgabe, herauszufinden, welche der Teilchendichten 1-6 zu welchen Bildern A-F gehören.