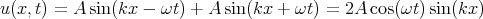
| Stehende Welle als Überlagerung gegenläufiger Wellen. Die rote Welle unten ist die Summe der beiden grünen Wellen oben. |
Dieser Film zeigt die Überlagerung zweier gegenläufiger Wellen mit gleicher Amplitude
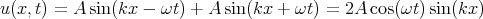
Die Überlagerung wird erzeugt, indem man einfach an jedem Punkt die Wellengrößen der einzelnen Wellen (die Auslenkungen) addiert.
Diese Überlagerung zweier fortlaufender Wellen ist selbst keine fortlaufende Welle, sondern eine sogenannte stehende Welle.
Es gibt Orte, an denen die Funktion u(x,t) immer verschwindet: u(xn,t) = 0 für alle t, mit xn = πn∕k. Diese Orte nennt man Schwingungsknoten. Überall sonst ändert sich die Auslenkung zeitlich periodisch.
Es gibt Zeiten, zu denen die Funktion u(x,t) überall verschwindet: u(x,tn) = 0 für alle x, mit tn = πn∕ω.
Stehende Wellen sind also zeitlich periodische Vorgänge (Schwingungen) mit räumlich feststehenden ("stationären") Schwingungsknoten.