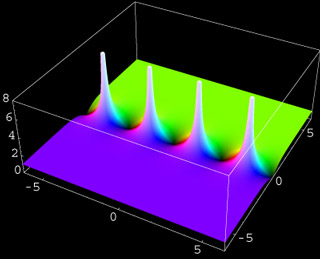
08
tan(z)
Show
2-d plot
The complex tangent function is defined (like in the real case) as the ratio between the sine and cosine functions. Thus tan(z) has a zero wherever sine has a zero and a pole wherever cosine has a zero. All zeros and poles are of first order. The complex tangent is the unique analytic continuation of the real tangent function. The values of tan(z) for z on the real axis are just given by the ordinary tangent function.
