Der Zustand mit der niedrigst-möglichen Energie ist sphärisch symmetrisch. Die Wellenfunktion ist strenggenommen überall ungleich Null, fällt aber nach außen hin rasch ab, sodass die Wahrscheinlichkeit, das Elektron weit weg vom Atomkern zu finden, extrem klein ist.

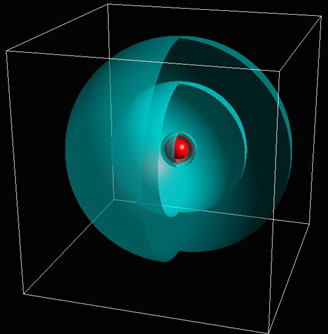
Es gibt insgesamt 4 Zustände zu dieser Energie. Diese unterscheiden sich durch die Drehimpuls-Quantenzahlen l und m. Der Zustand mit l=0 ist wieder sphärisch symmetrisch. Die Wellenfunktion ist Null auf einer Kugelschale um den Atomkern. Diese Kugelschale sitzt zwischen dem roten=positiven und dem blaugrünen=negativen Teil der Wellenfunktion. Sie ist ein stationärer "Schwingungsknoten" für diese stehende Welle.

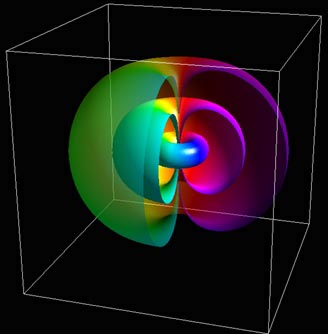
Torusförmige Wahrscheinlichkeitsverteilung. Beim Zustand mit m=-1 erscheinen die Farben entlang der Torusflächen in umgekehrter Reihenfolge. Die Wellenfunktion ist Null entlang der z-Achse.

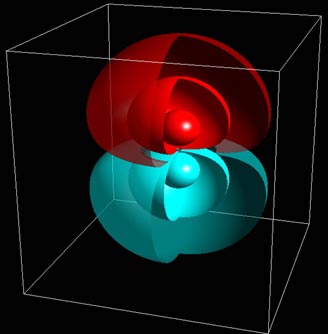
Hantelförmige Wahrscheinlichkeitsverteilung. Zustände mit m=0 haben immer Rotationssymmetrie um die vertikale z-Achse. Hier bildet die horizontale xy-Ebene einen stationären "Schwingungsknoten". Dort ist die Wellenfunktion Null.